Alan Turing is one of the smartest man of the 20th century. When he was not hacking Nazi crypto, defining the theory of computation or inventing tests for artificial intelligence he was interested on how the leopard got his spots...
In it's article "The Chemical Basis of Morphogenesis" he invented a system, called "reaction diffusion", which he suggested could be the basis of the development of patterns and shapes in biological organisms.
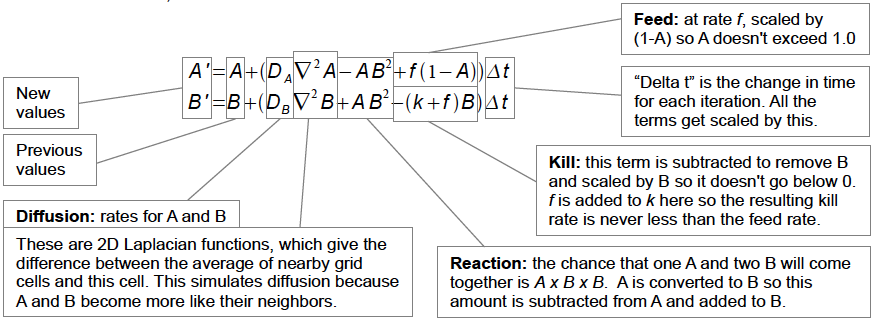
It is a system of partial differential equations that model a catalytic chemical reaction. There are two chemicals A and B. A is a catalyst that produces A and B, and B is a inhibitor that slows A activity. They are linked in a feedback loop, and when they diffuse trough a medium at different rates, they create patterns due to a kind of resonance and self-oscillation between the two chemicals.
Turing didn't had the computer power in the 1950's to simulate this, but had the intuition that this could work, and it was proven recently that Nature use systems like these to generate patterns. About the same time (but without knowing each other) the Russian scientist Boris Belousov, was working with the same ideas, but with actual chemicals, in a system that was later known as the Belousov–Zhabotinsky reaction.
The common thing between the two systems is that they escape thermodynamical equilibrium (which means stability and dead) by creating feedback loops which are cycles in phase space. These cycles in the dynamical properties of the system allows them to escape maximum entropy and remain in a non-equilibrium state.
I think this is the path to generating form. The ability to design dynamical systems that have properties that allows them to remain in a kind of non-equilibrium stability, or metastability. The real challenge is to find the right properties to not only generate form, but doing so in a recursive way creating every increasing layers of complexity.
Here is a little example of a reaction diffusion system. The screen is divided in 9 parts, that you can explore with your mouse. Each part is a different pattern generated with the same system.